R package spatialRF
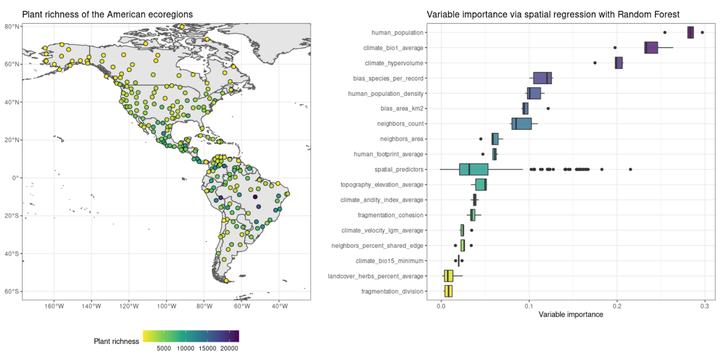 Graph by Blas M. Benito
Graph by Blas M. Benito
The package spatialRF trains explanatory spatial regression models by combining Random Forest with spatial predictors that help the model reduce the spatial autocorrelation of the residuals and return honest variable importance scores.
The package is designed to minimize the code required to fit a spatial model from a training dataset, the names of the response and the predictors, and a distance matrix, as shown in the mock-up call below.
m <- spatialRF::rf_spatial(
data = df,
dependent.variable.name = "response",
predictor.variable.names = c("pred1", "pred2", ..., "predN"),
distance.matrix = distance_matrix
)
spatialRF uses the fast and efficient ranger package under the hood
(Wright and Ziegler 2017), so please, cite the ranger package when using spatialRF!
This package also provides tools to identify potentially interesting variable interactions, tune random forest hyperparameters, assess model performance on spatially independent data folds, and examine the resulting models via importance plots, response curves, and response surfaces.
To learn more, please visit the package’s website.